
by Pierre Loidreau
<pierre.loidreau(at)ensta.fr>
About the author:
Pierre works as a Teacher-Researcher at the ENSTA (Ecole
Nationale Supérieure de Techniques Avancées). His
research field concerns "cryptosystems" based on the theory of
error correction codes. He "plays" with Linux everyday... and
tennis quite often.
Translated to English by:
Axelle Apvrille <axellec(at)netcourrier.com>
Content:
|
Introduction to cryptography

Abstract:
This article was first published in a Linux Magazine France
special issue focusing on security. The editor, the authors, the
translators kindly allowed LinuxFocus to publish every article from
this special issue. Accordingly, LinuxFocus will bring them to you
as soon as they are translated to English. Thanks to all the people
involved in this work. This abstract will be reproduced for each
article having the same origin.
Why cryptography - 2500 years of history.
The origin of cryptography probably goes back to the very
beginning of human existence, as people tried to learn how to
communicate. They consequently had to find means to guarantee
secrecy as part of their communications. However, the first
deliberate use of technical methods to encipher messages may be
attributed to the ancient Greeks, around 6 years BC: a stick, named
"scytale" was used. The sender would roll a strip of paper around
the stick and write his message longitudinally on it. Then, he'd
unfold the paper and send it over to the addressee. Decrypting the
message without knowledge of the stick's width - acting here as a
secret key - was meant to be impossible. Later, Roman armies used
Caesar's cipher code to communicate (a three letter alphabet
shift).
The next 19 centuries have been devoted to creating more or less
clever experimental encipher techniques, whose security actually
relied on how much trust user would grant them. During the 19th
century, Kerchoffs wrote the principles of modern cryptography. One
of those principles stated that security of a cryptographic system
did not rely on the cryptographic process itself but on the key
that was used.
So, from that point, cryptographic systems were expected to meet
those requirements. However, existing systems still lacked
mathematical background, and therefore tools to measure or
benchmark their resistance to attacks. Even better if somebody
could finally reach cryptographic's ultimate goal and find a 100%
unconditionally safe system ! In 1948 and 1949, scientific
background was added to cryptography with 2 papers of Claude
Shannon: "A Mathematical Theory of Communication" and mainly "The
Communication Theory of Secrecy Systems". Those articles swept away
hopes and prejudices. Shannon proved Vernam's cipher that had been
proposed a few years before - and also named One Time Pad -- was
the only unconditionally safe system that could ever exist.
Unfortunately, that system was unusable in practice... This is the
reason why, nowadays, evaluation of security systems is based on
computational security instead. One claims a secret key cipher is
safe if no known attack's complexity is any better than a full
search on all possible keys.
AES (Advanced Encryption Standard)
Recently, in October 2000, the NIST (National Institute of
Standards and Technology) announced the approval of a new secret
key cipher standard chosen among 15 candidates. This new standard
algorithm was meant to replace the old DES algorithm, whose key
sizes were becoming too small. Rijndael - a compressed name taken
from its inventors Rijmen and Daemen - was chosen to become the
future AES.
This encryption system is said to be a "block" cipher as messages
are enciphered by entire 128-bit block units. Multiple options
exist proposing the use of 128, 192 or 256 bit keys. Just for your
information, DES enciphers 64 bit blocks with a key of only 56
bits. Triple DES usually enciphers 64 bit blocks with a 112-bit
key.
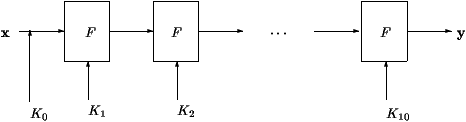
Table 1: AES iterations
AES operational mode is described at figure 1. First, a secret key
K0 is XORed bitwise to the message. Then, similarly to all block
ciphers, a function F is iterated, using subkeys generated by a key
expansion routine initialized by the master key.
For AES, function F is iterated 10 times.
- Figure 2 describes how function F is iterated for encryption.
A 128-bit block spans 16 bytes taken as input. First, substitution
S is applied to each byte. Then, a second permutation P is
applied to the 16 bytes. The 128-bit subkey generated by the key
expansion routine is then added bitwise to the previous
result.
- Key Ki of round n°i is obtained from the key expansion
routine using subkey K(i-1) of round n°i-1 and K0 the secret
key. The key expansion routine is described at figure 3. The 16
bytes of key K(i-1) are processed 4 by 4.
The last 4 bytes are permuted using substitution S - the same
substitution that is used in iterated function F to substitution bits
of each byte. Then, the first 4 resulting bytes is added to
alpha' element. This element is a pre-defined byte which depends
on round number. Finally, to obtain Ki, the resulting 4 bytes are
added bitwise to the first 4 bytes of K(i-1). Then the result is
added to the next four bytes etc.

Table 2: Function F
Now, let's see briefly how substitutions are built, and what
constant ai is intended for. Technically - and for
simplicity reasons - a byte should be considered as an element of a
set of 256 elements, called a finite field, and onto which all
sorts of simple operations (such as addition, multiplication and
inverse) exist. As a matter
of fact, substitution S mentioned previously is an inverse in such
a field. Substitution S is specified as a very simple operation and
can consequently be easily implemented. Element ai
corresponds to elevation to power i of an element of the field.
Such considerations make AES implementations very efficient.
As AES is only built upon simple bytewise operations, this
provides it with two major advantages:
- even pure software implementations of AES are very quick. For
example, a C++ implementation on a Pentium 200Mhz offers a
70Mbits/s encryption performance ;
- resistance of AES to differential and linear cryptanalysis
does not depend on choice of S-Box, as for DES where those
S-Boxes had been suspected to contain a backdoor for NSA. As a
matter of fact, all operations are simple.
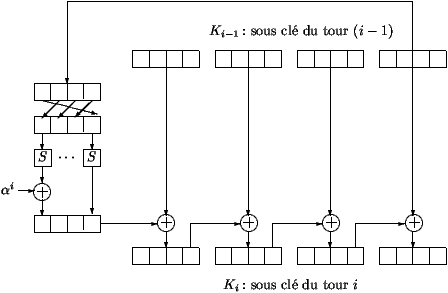
Table 3: Key expansion routine
Public key cryptography
In 1976, Diffie and Hellman published an article "New Directions in
Cryptography" which was a real scoop to the cryptographers
community. This article introduces the concept of public key
cryptography. Actually, the only family of algorithms known at that
time - symmetric secret key algorithms - could no longer satisfy
the new needs that had appeared due to the burst in communications
methods such as networks.
Basically, the core of their novel idea was to introduce the
concept of trapdoor one-way functions. Such functions are easy to
operate in one way, but are computationally infeasible to invert
without knowing the secret trap - even though the function itself
is known by all. Then, the public key acts as the function, whereas
the trap (only known by a limited number of users) is called a
private key. This gave birth to the world of Alice and Bob (and
others). Alice and Bob are two persons who try to communicate with
integrity requirements, defeating intruders which might try to
listen, eavesdrop or alter communication.
Of course, to decipher the message, the recipient just needs to
invert the function, using the secret trap.
The nicest example of public key cryptosystem (and undoubtedly the
simplest) was presented two years later in 1978. It was invented by
Rivest, Shamir and Adleman and is therefore shortened RSA. It is
based on the mathematical difficulty of integer factorization. The
private key is made out of the triplet (p,q,d) with p and q
two primes (having roughly same size), and d a relative prime to
p-1 and q-1. The public key is made of pair (n,e), with
n=pq, and e the inverse of d modulus (p-1)(q-1), i.e.
ed = 1 mod(p-1)(q-1).
Suppose Alice wants to send some text, enciphered with Bob's public
key (n,e). She first transforms the message in an integer m less
than n. Then, she processes
c = me mod
n,
and sends the result c over to Bob. On his side, Bob whose private
key is (p,q,d) processes :
cd mod n =
med mod n =
m.
For RSA, the one-way trap function is the function which associates
an integer x <n to the value xe mod n.
Since RSA, many other public key cryptosystems have been invented.
Currently, one of the most famous alternatives to RSA is a
cryptosystem based on discrete logarithms.
Modern use of cryptography
Actually, public key cryptography is really interesting because it
is easy to use and it solves many security problems heretofore
unsolved. More precisely, it solves a few authentication problems:
- Identifying individuals: using anonymous
communications means of today, Alice wants to be sure the person
with whom she is talking is not cheating and impersonating Bob.
To do so, she uses an identification protocol. Multiple
identification protocols exist and commonly rely on the
principles of RSA or of discrete logarithm.
- Document authentication: an authority authenticates
documents through a digital signature. Signing consists in
appending a few bits which are the result of some processing with
document and authority as input, and which are generally hashed
by a hash algorithm such as MD5 or SHA. Moreover, any person with
access to the document should be able to verify that signature
has really been issued by the authority. To do so, signature
schemas are used. One of the most famous signature scheme is
ElGamal - once more based on discrete logarithm problems.
Besides, as secret key cryptography, public key cryptography
provides encryption-based cryptosystems, guaranteeing
confidentiality of communications.
Let's imagine Alice wants to communicate secretly with Bob. Alice
retrieves Bob's public key in a public directory, and enciphers her
message with this key. When Bob receives the ciphertext, he uses
his private key to decipher the ciphertext and read initial clear
text. Both keys have very different roles, this explains why such
systems are called asymmetric cryptosystems - referring to secret
key cryptosystems which use the same key for ciphering and
deciphering and are also know as symmetric cryptosystems.
Public key cryptography offers another major benefit over secret
key cryptography. As a matter of fact, if n users communicate
through a secret key cryptosystem, each of them need one different
secret key for each person in the group. So, n(n-1) keys need to be
managed. If n is over thousands of users, then millions of keys
need to be managed... Furthermore, adding a new user to the group
is not an easy task, because n new keys need to be generated for
the user to communicate with all members of the group. Then, those
new keys need to be sent over to the group. On the contrary, in
asymmetric cryptosystems, the n public keys of the members are
stored in a public directory. Adding a new user simply consists in
adding his public key to the directory.
Using a public or a secret key: finding a trade-off
The previous paragraph has explained that public key cryptography
solved many problems secret key cryptography could not cope with.
One might then wonder what for AES has been designed. Actually,
there are two major explanations to this choice.
- First, a practical reason. Generally, public key
cryptosystems are very slow. For instance, software
implementations of RSA are a thousand times slower than AES, and
RSA has not been designed with hardware implementation in mind.
Transmitting information is so crucial today, we cannot accept to
be limited by a cipher algorithm.
- Second, public key cryptosystems' inner structure lead to
other security problems.
For instance, public key cryptosystems require much larger key
sizes - for a correct security level - than secret key
cryptosystems. Actually, the notion and importance given to key
length should only be considered in secret key cryptosystems. As
a matter of fact, those systems rely on the fact that only
brute-force attacks might defeat them, i.e. enumerating all
possible keys. If key length is 128 bits, then 2128 should be enumerated.
But with public key cryptosystems, key size is only an
interesting parameter when considering the same system. For
instance, RSA with a 512 bit key is less secure than AES with a
128 bit key. The only way to correctly evaluate a public key
cryptosystem is to assess the complexity of the best known
attack, and this is quite different: one never knows if a new
invention is going to compromise the system's security. Recently,
a group of researchers successfully factored a 512 bit integer.
Consequently, for a correct security level, the usual advice is
to use 1024 bit numbers.
As a consequence, for pure encipherment, secret key algorithms are
preferred - when it's possible to use them. Zimmermann has worked
over an interesting hybrid solution, implemented in PGP. Basically,
when Alice and Bob want to communicate with integrity features,
using a secret key algorithm (PGP uses IDEA):
- Alice and Bob negotiate a secret key using a key exchange
protocol. Key exchange protocols use public key cryptography. One
of the most famous protocols relies on Diffie-Hellman's
algorithm.
- Then, they communicate using the IDEA algorithm.
When they have finished communicating, the negotiated session key
is discarded. Such a system uses both secret key cryptosystems and
public key cryptosystems. Usually, people consider the less secure
part of such a system is the key exchange protocol.
Bibliography
History of cryptography :
- S. Singh : Histoire des codes secrets. Jean-Claude
Lattès, 1999.
- D. Kahn : The Codebreakers: the story of secret
writing. MacMillan publishing, 1996.
For AES :
Cryptography in general :
Talkback form for this article
Every article has its own talkback page. On this page you can submit a comment or look at comments from other readers:
2002-05-15, generated by lfparser version 2.28




