[hp15c]

HP15c software: quadratic equation solver, x2+p*x+q=0


command      display

f LBL C        001-42,21,13
   x><y         002-      34
   2            003-       2
   CHS          004-      16
   /            005-      10
   Enter        006-      36
   *            007-      20
g LST X        008-43    36
g LST X        009-43    36
   R_arrow_down 010-      33
   R_arrow_down 011-      33
   x><y         012-      34
   -            013-      30
   square root  014-      11
   R_arrow_down 015-      33
g LST X        016-43    36
   square root  017-      11
   -            018-      30
   x><y         019-      34
g LST X        020-43    36
   +            021-      40
g RTN          022-   43 32

This program uses the following label: LBL C

Using the program

I start every program with a label. This way you can have a number of programs in your 15c and you just select which one to run by pressing f LABELNAME (f C in this case) or GSB LABELNAME (GSB C in this case).

This program finds the points x1 and x2 on the X-axis where the graph y=x2+p*x+q intersects with the X-axis.


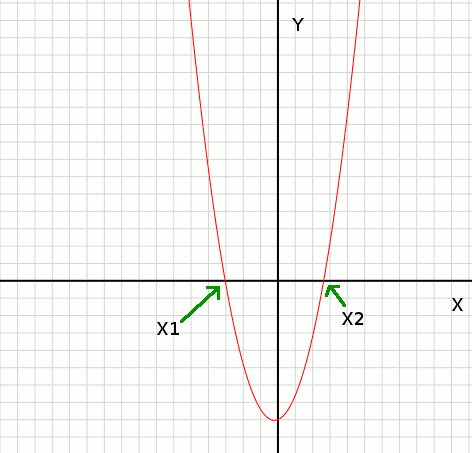
graph: y=x2+p*x+q

Let's say you would like to know The solutions of x2 + 0.5*x - 3=0

This means p=0.5 and q=-3. p goes into the y register of the stack and q into the x register of the stack (the x register is equal to the display line).
You type: 0.5, ENTER, 3, CHS, GSB C
The display shows "running" and then you see 1.5. This is one solution to the quadratic equation and you see the other one by pressing the "x><y" (swap x and y stack registers): x2=1.5 x1=-2

It is possible that the quadratic equation has no solution (if you move the parabola above the X-axis such that there is no intersection with the X-axis). In this case you will see "Error 0" in the display.

Algorithm

x2 + p*x + q=0 has the following 2 solutions:

x1=-p/2 - sqrt((p/2)2 - q)
x2=-p/2 + sqrt((p/2)2 - q)


Note that the HP15c has as well the f SOLVE function but this program is useful if you have to solve quadratic equations frequently.
© Guido Socher