
![[Photo of the Author]](../../common/images/Miguel-S.jpg)
original in en Miguel A Sepulveda
![[OpenGL logo]](../../common/January1998/ogl.gif)
This is the first article in a series on OpenGL, an industry standard for 2D/3D graphics (see also What is OpenGL). We will assume that the reader is familiar with his/hers C development platform, and has some knowledge of the GLUT library (otherwise just follow the "GLUT programming" series of articles in this magazine). Under Linux we recommend the usage of the Mesa-library which is a wonderful freeware implementation of OpenGL. Now there is even hardware support for Mesa (see 3Dfx graphics card).
Every presentation of new OpenGL commands will be accompanied by an example that tries to exploit its functionality, at least we will try !. By the end of our series we will present you with the source code of a game simulation completely written in OpenGL.
Before getting started I would like to mention that since I am a scientist, most of my experience with OpenGL is as a tool to write simulations of real quantum and classical systems. So my examples are a bit bias ;-). I hope readers find these examples accessible or at least amusing. If you would like to see other kinds of examples just let me know.
OpenGL is often associated with 3D graphics, fancy special effects, complex models with realistic light modeling etc.. However it is also a 2D graphics rendering machine. This is important because there are many things you can learn to do in 2D before starting to learn about the complexities of 3D perspectives, model rendering, lights, camera position, etc.. A large number of engineering and science applications can be render in 2D. So let us first learn how to do some simple 2D animations.
OpenGL has only a few geometric primitives: points, lines, polygons. All of them are described in terms of their respective vertices. A vertex is characterized by 2 or 3 floating points, the Cartesian coordinates of the vertex, (x,y) in 2D and (x, y, z) in 3D. While Cartesian coordinates are the most common, in computer graphics there is also the homogeneous coordinate system in which every point is described by 4 floating points (x, y, z, w). We will come back to them after covering some elementary notions of 3D rendering.
Since in OpenGL all geometric objects are eventually described as an ordered set of vertices, there is a family of routines to declare a vertex. Its syntax is:
void glVertex{234}{sifd}[v](TYPE coords);
Get familiar with this notation. The curly brackets indicate part of the name of the routine. The routines can take 2, 3 or 4 parameters in either short, long, float or double type. Optionally these parameters can be supplied in a vector form, in which case we would use the v-type routines. Here are some examples:
void glVertex2s(1, 3);
void glVertex2i(23L, 43L);
void glVertex3f(1.0F, 1.0F, 5.87220972F);
float vector[3];
void glVertex3fv(vector);
To simplify all these routines are refered to as glVertex*.
OpenGL interprets any sequence of vertices according to its
context. The context is declared by the pair of routines
glBegin(GLenum mode) and
glEnd(), any glVertex*
statements executed between the two are interpreted according
to the value of mode, for example:
glBegin(GL_POINTS);
glVertex2f(0.0, 0.0);
glVertex2f(1.0, 0.0);
glVertex2f(0.0, 1.0);
glVertex2f(1.0, 1.0);
glVertex2f(0.5, 0.5);
glEnd();
draws 5 points in 2D with the coordinates specified. GL_POINTS is one of the labels defined in the OpenGL header file <GL/gl.h>. There are many other modes available but we will review then as necessary.
Every point is drawn with the color currently stored in the
OpenGL state variable associated with the color buffer. To
change the current color, use the family of routines
glColor*; there is a lot to say about selecting
and manipulating colors (there will be another article only on
this subject). For the moment, we will be using three floating
point numbers from 0.0 to 1.0 - this is the RGB
(Red-Green-Blue) encoding;
glColor3f(1.0, 1.0, 1.0); /* White */
glColor3f(1.0, 0.0, 0.0); /* Red */
glColor3f(1.0, 1.0, 0.0); /* Magenta */
etc...
This is already enough material to write our first two examples of code. The first example is a simple OpenGL program that draws a number of orbits in a chaotic map (The standard map). If the reader is not familiar with mappings and the standard map in particular, it does not matter. To put it simply, a map takes a point and generates a new one using a well defined formula:
yn+1 = yn + K
sin(xn)
xn+1 = xn + yn+1
In the case of the standard map it represents a model for the trace left by a charged particle that circles around the tori of an accelerator of particles and crosses a section plane of the accelerator. Studying the properties of this and other maps is important in physics because it helps us understand the stability of the charged particle confined in the cyclotron. The standard map is very cool because for some values of its parameter, K clearly shows a mixture of chaotic and trapped motion. Finally even those who are not really interested in physics but still want to develop some nice graphics code should pay some attention to maps and their properties, many of the algorithms for generating textures, fire flares, trees, terrain, etc.. are based on fractal maps.
Here is the code example1.c:
#include <GL/glut.h>
#include <math.h>
const double pi2 = 6.28318530718;
void NonlinearMap(double *x, double *y){
static double K = 1.04295;
*y += K * sin(*x);
*x += *y;
*x = fmod(*x, pi2);
if (*x < 0.0) *x += pi2;
};
void winInit(){
/* Set system of coordinates */
gluOrtho2D(0.0, pi2, 0.0, pi2);
};
void display(void){
const int NumberSteps = 1000;
const int NumberOrbits = 100;
const double Delta_x = pi2/(NumberOrbits-1);
int step, orbit;
glColor3f(0.0, 0.0, 0.0);
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0, 1.0, 1.0);
for (orbit = 0; orbit < NumberOrbits; orbit++){
double x, y;
y = 3.1415;
x = Delta_x * orbit;
glBegin(GL_POINTS);
for (step = 0; step < NumberSteps; step++){
NonlinearMap(&x, &y);
glVertex2f(x, y);
};
glEnd();
};
for (orbit = 0; orbit < NumberOrbits; orbit++){
double x, y;
x = 3.1415;
y = Delta_x * orbit;
glBegin(GL_POINTS);
for (step = 0; step < NumberSteps; step++){
NonlinearMap(&x, &y);
glVertex2f(x, y);
};
glEnd();
};
};
int main(int argc, char **argv) {
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGBA);
glutInitWindowPosition(5,5);
glutInitWindowSize(300,300);
glutCreateWindow("Standard Map");
winInit();
glutDisplayFunc(display);
glutMainLoop();
return 0;
}
Please read the Programming GLUT
article to understand the glut* routines, most of this code
came from there. The graphics window is opened in single buffer
and RGB mode. Then a callback function named display() draws the map: first we select the
color black for the background; glClear(GL_COLOR_BUFFER_BIT)
resets the color buffer to the current color (black), next
after selecting white color with glColor, we run the NonlinearMap() a number of times and
plot the points with glVertex* in GL_POINTS mode. Really
simple.
Notice that in the window initialization routine winInit() there is a single statement
from the OpenGL Utility toolkit, gluOrtho2D(). This
routine sets a 2D orthogonal system of coordinates. The
parameters passed are "minimum x, maximum x, minimum y, maximum
y".
I have chosen a single mode window and a large number of points
so that you have a chance to see the image as it is being
drawn. This is common of single mode with large and time
consuming images, things appear on your screen as they are
invoked with OpenGL routines.
After running ../../common/January1998/example1 you should see this image:

Let's go now to the second program, example2.c:
#include <GL/glut.h>
#include <math.h>
const double pi2 = 6.28318530718;
const double K_max = 3.5;
const double K_min = 0.1;
static double Delta_K = 0.01;
static double K = 0.1;
void NonlinearMap(double *x, double *y){
/* Standard Map */
*y += K * sin(*x);
*x += *y;
/* Angle x is module 2Pi */
*x = fmod(*x, pi2);
if (*x < 0.0) *x += pi2;
};
/* Callback function:
What to do in absence of use input */
void idle(void){
/* Increase the stochastic parameter */
K += Delta_K;
if(K > K_max) K = K_min;
/* Redraw the display */
glutPostRedisplay();
};
/* Initialization for the graphics window */
void winInit(void){
gluOrtho2D(0.0, pi2, 0.0, pi2);
};
/* Callback function:
What to do when the display needs redrawing */
void display(void){
const int NumberSteps = 1000;
const int NumberOrbits = 50;
const double Delta_x = pi2/(NumberOrbits-1);
int step, orbit;
glColor3f(0.0, 0.0, 0.0);
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0, 1.0, 1.0);
for (orbit = 0; orbit < NumberOrbits; orbit++){
double x, y;
y = 3.1415;
x = Delta_x * orbit;
glBegin(GL_POINTS);
for (step = 0; step < NumberSteps; step++){
NonlinearMap(&x, &y);
glVertex2f(x, y);
};
glEnd();
};
for (orbit = 0; orbit < NumberOrbits; orbit++){
double x, y;
x = 3.1415;
y = Delta_x * orbit;
glBegin(GL_POINTS);
for (step = 0; step < NumberSteps; step++){
NonlinearMap(&x, &y);
glVertex2f(x, y);
};
glEnd();
};
glutSwapBuffers();
};
int main(int argc, char **argv) {
/* GLUT Initializations */
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGBA);
glutInitWindowPosition(5,5);
glutInitWindowSize(300,300);
/* Open Window */
glutCreateWindow("Order to Chaos");
/* Window initializations */
winInit();
/* Register callback functions */
glutDisplayFunc(display);
glutIdleFunc(idle);
/* Launch event processing */
glutMainLoop();
return 0;
}
This program is based on ../../common/January1998/../../common/January1998/example1.c,
the main difference is that the window is opened in a double
buffer mode, and the map parameter K is a variable that changes
during the life of the program. There is a new callback
function idle() registered to the
GLUT event processor by glutIdleFunc(). This function
has a special meaning; it gets run every so often by the event
processor in the absence of user input. The idle()
callback function is ideal for programming animations. In
../../common/January1998/example2, it serves the purpose of
changing slightly the value of the map parameter. At the end of
idle() there is another useful GLUT statement,
glutPostResDisplay() which redraws the window preserving
the previous window's initializations. In general, it is more
efficient than simply calling display() again.
Another difference worth noticing is the use of glutSwapBuffers() at the end of display(). The window was initialized in double buffer mode, therefore all the rendering directives are applied to the hidden buffer; the user cannot see the image being draw in this case. After the whole image (frame) has been finished then it is made visible by switching hidden and visible buffers with glutSwapBuffers(). Without this technique the animation will not run smoothly.
Here are some of the frames displayed during the animation:

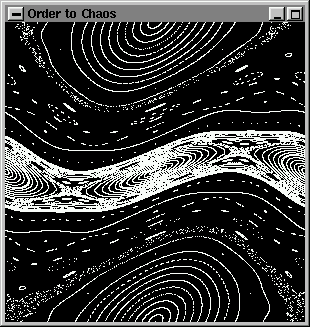

IMPORTANT: The display() callback function always gets invoked at least once, before idle(). Keep this in mind when writing your animations and deciding what goes to display() and what to idle().
As previously mentioned glBegin(GLenum mode) accepts various modes and the sequence of vertices v0, v1,v2, v3,v4,... vn-1 declared afterwards are interpreted accordingly. The possible values for mode and the actions taken are:
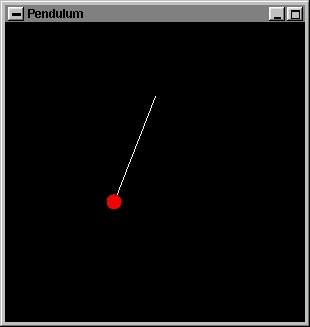
As before there is an idle() callback function whose aim here is to keep the clock running (updating the variable time). The display() draws two objects; the pendulum cord and weight (in white and red respectively). The motion of the pendulum coordinates is implicit in the formulas for xcenter and ycenter:
void display(void){
static double radius = 0.05;
const double delta_theta = pi2/20;
double xcenter , ycenter;
double x, y;
double theta = 0.0;
double current_angle = cos(omega * time);
glColor3f(0.0, 0.0, 0.0);
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0, 1.0, 1.0);
/* Draw pendulum cord */
glColor3f(1.0, 1.0, 1.0);
glBegin(GL_LINES);
glVertex2f(0.0, 0.0);
xcenter = -cord_length * sin(current_angle);
ycenter = -cord_length * cos(current_angle);
glVertex2f(xcenter, ycenter);
glEnd();
/* Draw pendulum dish */
glColor3f(1.0, 0.0, 0.0);
glBegin(GL_POLYGON);
while (theta <= pi2) {
x = xcenter + radius * sin(theta);
y = ycenter + radius * cos(theta);
glVertex2f(x, y);
theta += delta_theta;
};
glEnd();
glutSwapBuffers();
};
Here are some suggestions for practicing what you have learned so far:
This is all for now. There are still many things to discuss
about polygons. In the next issue (March 1998) we will continue
to explore polygons, modeling and cover in more detail some of
the commands your are already familiar with.